Welcome to the captivating realm of AP Calculus Unit 1 Progress Check MCQ Part B! This section delves into the foundational concepts of calculus, equipping you with a comprehensive understanding of functions, limits, derivatives, and their myriad applications.
Embark on a journey through the intricacies of different function types, mastering techniques for graphing them and identifying their key features. Explore the profound significance of limits and continuity, unlocking the secrets of evaluating limits and discerning the behavior of functions.
Discover the power of derivatives, unlocking their potential to solve real-world problems and analyze complex mathematical phenomena.
Unit 1 Progress Check MCQ Part B Overview
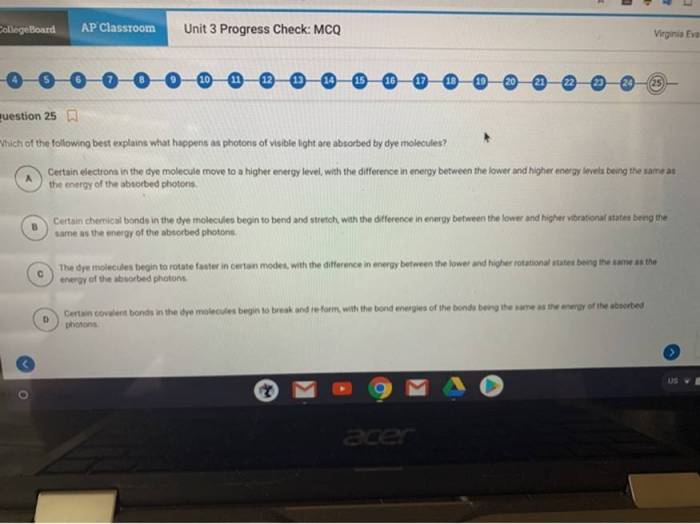
Unit 1 Progress Check MCQ Part B assesses students’ understanding of fundamental concepts in calculus, including functions, limits, continuity, derivatives, and their applications. It provides insights into students’ grasp of the key ideas covered in Unit 1 and helps identify areas where further support or reinforcement may be needed.
This section covers a wide range of topics, including:
- Different types of functions and their graphs
- Limits and methods for evaluating them
- Concept of continuity and its relationship to limits
- Derivatives and their significance
- Methods for finding derivatives
- Applications of derivatives in various fields
Functions and Their Graphs
Functions are mathematical relationships that assign a unique output value to each input value within a given domain. In Unit 1, students encounter different types of functions, including:
- Linear functions: f(x) = mx + b
- Quadratic functions: f(x) = ax² + bx + c
- Polynomial functions: f(x) = a nx n+ a n-1x n-1+ … + a 1x + a 0
- Rational functions: f(x) = p(x) / q(x), where p(x) and q(x) are polynomials
- Exponential functions: f(x) = a x, where a is a positive constant
- Logarithmic functions: f(x) = log ax, where a is a positive constant
To graph functions, students use various techniques, such as:
- Plotting points
- Using symmetry
- Finding intercepts and asymptotes
- Applying transformations
Key features of function graphs include:
- Intercepts: Points where the graph crosses the x-axis or y-axis
- Asymptotes: Lines that the graph approaches but never touches
- Extrema: Maximum and minimum points of the graph
Limits and Continuity: Ap Calculus Unit 1 Progress Check Mcq Part B
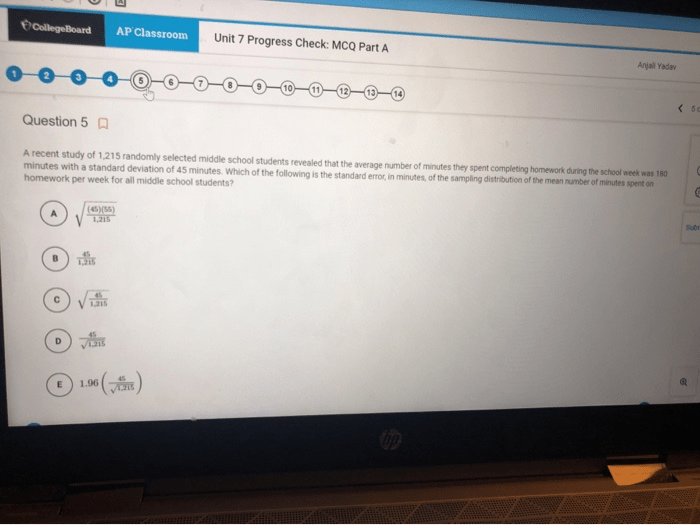
Limits describe the behavior of a function as the input value approaches a specific value or infinity. They are essential for understanding the concept of continuity.
Methods for evaluating limits include:
- Direct substitution
- Factoring
- Rationalization
Continuity refers to the smoothness of a function’s graph at a given point. A function is continuous at a point if its limit at that point exists and equals the function’s value at that point.
Derivatives
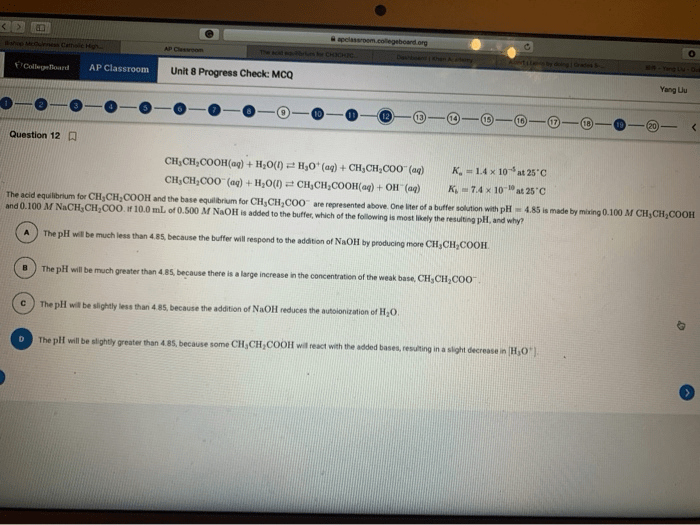
Derivatives measure the rate of change of a function with respect to its input variable. They have numerous applications in calculus and other fields.
Methods for finding derivatives include:
- Power rule
- Product rule
- Quotient rule
Derivatives can be used to:
- Find extrema (maximum and minimum points)
- Analyze the shape of graphs
- Solve optimization problems
Applications of Derivatives
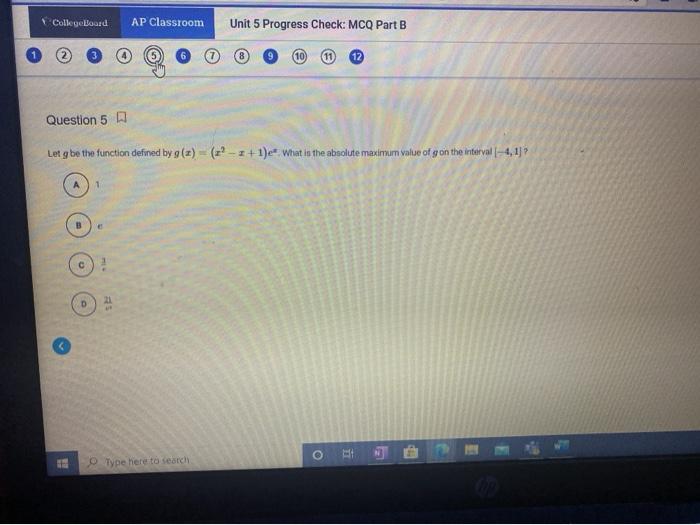
Derivatives have wide-ranging applications in various fields, including:
- Mathematics:Finding critical points, analyzing concavity, determining intervals of increase/decrease
- Physics:Calculating velocity, acceleration, and displacement
- Economics:Analyzing marginal cost, revenue, and profit functions
- Optimization:Finding the best possible solution to a problem, such as minimizing cost or maximizing profit
Essential Questionnaire
What is the purpose of the AP Calculus Unit 1 Progress Check MCQ Part B?
This section assesses your understanding of the core concepts covered in Unit 1 of AP Calculus, including functions, limits, derivatives, and their applications.
How can I prepare for the AP Calculus Unit 1 Progress Check MCQ Part B?
Thoroughly review the concepts covered in Unit 1, practice solving problems related to functions, limits, derivatives, and their applications, and utilize practice tests to simulate the actual assessment.