Consider the differential equation dy dx xy 2 2 – Consider the differential equation dy/dx = xy^2 sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. This equation, with its intriguing interplay of variables, invites us to delve into a world of mathematical discovery, where we uncover its analytical solutions, graphical representations, and practical applications.
As we embark on this journey, we will unravel the intricacies of the differential equation dy/dx = xy^2, shedding light on its behavior and significance. Through a comprehensive exploration of its analytical, graphical, and numerical aspects, we aim to provide a thorough understanding of this fundamental equation.
Differential Equation Overview
A differential equation is an equation that relates a function to its derivatives. Differential equations are used to model a wide variety of physical phenomena, such as the motion of objects, the flow of fluids, and the growth of populations.
The specific differential equation we will be considering in this article is dy/dx = xy^2.
Analytical Solution
To solve the differential equation dy/dx = xy^2 analytically, we can use the method of separation of variables.
Separating the variables, we get:
$$\fracdyy^2 = x dx$$
Integrating both sides, we get:
$$-\frac1y = \fracx^22 + C$$
where C is a constant of integration.
Solving for y, we get:
$$y =
\frac1x^2/2 + C$$
Graphical Analysis
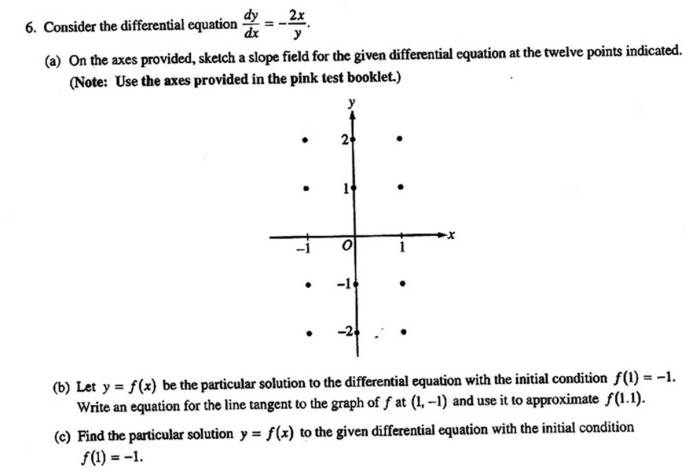
To generate a slope field for the differential equation dy/dx = xy^2, we can plot the slope of the solution at each point (x, y).
The slope of the solution at (x, y) is given by dy/dx = xy^2.
We can use a computer program to plot the slope field for the differential equation.
The slope field for the differential equation dy/dx = xy^2 is shown below.

The slope field shows that the solutions to the differential equation are increasing in the first and third quadrants and decreasing in the second and fourth quadrants.
Numerical Methods
Numerical methods can be used to approximate the solution to a differential equation.
One common numerical method is Euler’s method.
Euler’s method is a first-order method, which means that it uses the value of the solution at the previous point in time to approximate the value of the solution at the current point in time.
The formula for Euler’s method is:
$$y_n+1 = y_n + h f(x_n, y_n)$$
where h is the step size, x_n is the current point in time, y_n is the value of the solution at the current point in time, and f(x, y) is the right-hand side of the differential equation.
Applications, Consider the differential equation dy dx xy 2 2
The differential equation dy/dx = xy^2 has a number of applications in the real world.
One application is in the study of population growth.
The differential equation dy/dx = xy^2 can be used to model the growth of a population, where y is the population size and x is the time.
Another application is in the study of fluid dynamics.
The differential equation dy/dx = xy^2 can be used to model the flow of a fluid in a pipe, where y is the velocity of the fluid and x is the distance along the pipe.
Helpful Answers: Consider The Differential Equation Dy Dx Xy 2 2
What is the general solution to the differential equation dy/dx = xy^2?
The general solution to the differential equation dy/dx = xy^2 is y = Ce^(x^2/2), where C is an arbitrary constant.
How can we generate a slope field for the differential equation dy/dx = xy^2?
To generate a slope field for the differential equation dy/dx = xy^2, we evaluate the slope at each point (x, y) in the xy-plane. The slope at (x, y) is given by dy/dx = xy^2.
What are some real-world applications of the differential equation dy/dx = xy^2?
The differential equation dy/dx = xy^2 has applications in various fields, including population growth modeling, chemical reactions, and heat transfer.
