Identify the surface with the vector function – Embarking on a journey into the realm of surface identification using vector functions, this discourse unravels a tapestry of mathematical concepts and practical applications. Delving into the intricacies of vector functions, we will uncover their power in defining and characterizing surfaces, paving the way for a deeper understanding of their geometric properties and visualization.
As we progress, we will explore the mathematical underpinnings of surface identification, examining how vector functions provide a concise and elegant representation of surfaces. We will investigate techniques for extracting surface properties, such as normal vectors, tangent vectors, and curvature, from vector functions, gaining insights into the intrinsic geometry of surfaces.
1. Identify Surface Using Vector Function
In mathematics, a vector function is a function that assigns a vector to each point in a domain. Vector functions are often used to represent surfaces in three-dimensional space. To identify a surface using a vector function, we need to find a vector function that satisfies the following equation:
$$\bf r(u, v) = x(u, v)\bf i + y(u, v)\bf j + z(u, v)\bf k$$
where $\bf r(u, v)$ is the position vector of the point $(x, y, z)$ on the surface, and $u$ and $v$ are parameters that vary over the domain of the function.
For example, the following vector function represents a sphere of radius $a$ centered at the origin:
$$\bf r(u, v) = a\sin u \cos v\bf i + a\sin u \sin v\bf j + a\cos u\bf k$$
where $0 \le u \le \pi$ and $0 \le v \le 2\pi$.
2. Surface Properties from Vector Function
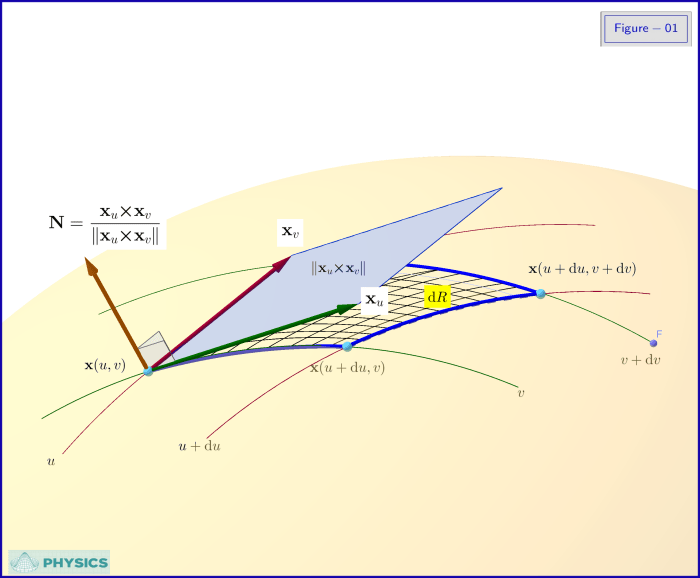
Once we have a vector function that represents a surface, we can use it to determine various surface properties. For example, we can find the normal vector to the surface at a given point by taking the cross product of the partial derivatives of the vector function with respect to $u$ and $v$:
$$\bf n(u, v) = \frac\partial\bf r\partial u \times \frac\partial\bf r\partial v$$
We can also find the tangent vectors to the surface at a given point by taking the partial derivatives of the vector function with respect to $u$ and $v$:
$$\bf t_u(u, v) = \frac\partial\bf r\partial u, \quad \bf t_v(u, v) = \frac\partial\bf r\partial v$$
The curvature of the surface at a given point can be calculated using the following formula:
$$k = \frac||\bf t_u \times \bf t_v|||\bf n|^3$$
3. Surface Visualization with Vector Function: Identify The Surface With The Vector Function
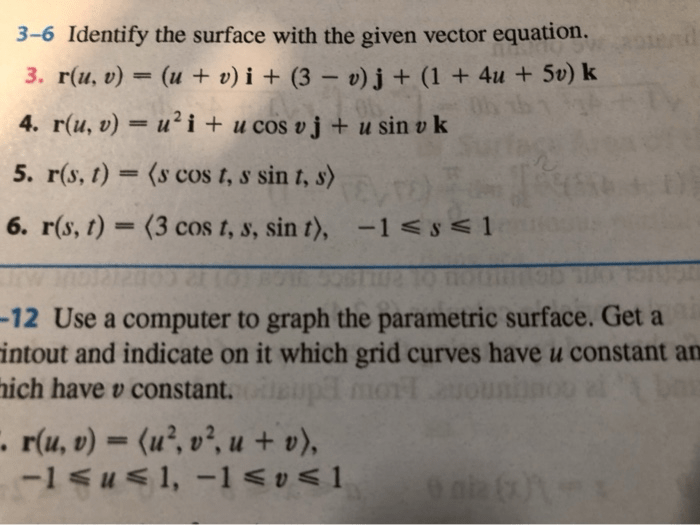
Vector functions can be used to visualize surfaces in a variety of ways. One common method is to use parametric plots. In a parametric plot, the parameters $u$ and $v$ are varied over their respective domains, and the corresponding values of $x$, $y$, and $z$ are used to generate a point in three-dimensional space.
The resulting collection of points forms a surface.
Another method for visualizing surfaces is to use contour plots. In a contour plot, the level curves of a function are plotted in the $xy$-plane. The level curves of a function are the curves that connect the points where the function takes on a constant value.
By plotting the level curves of a function, we can get a good idea of the shape of the surface that the function represents.
There are a number of software packages that can be used to generate parametric plots and contour plots of vector functions. Some of the most popular software packages include MATLAB, Mathematica, and Maple.
4. Applications of Surface Identification
Identifying surfaces with vector functions is a crucial step in a wide range of applications. In engineering, vector functions are used to model the surfaces of objects such as airplanes, cars, and buildings. In physics, vector functions are used to model the surfaces of waves and other physical phenomena.
In computer graphics, vector functions are used to model the surfaces of objects in virtual worlds.
Here are some specific examples of how vector functions are used in real-world applications:
- In engineering, vector functions are used to design the surfaces of aircraft wings. The shape of an aircraft wing is critical to its aerodynamic performance, and vector functions allow engineers to design wings that are both efficient and safe.
- In physics, vector functions are used to model the surfaces of waves. The shape of a wave is determined by the wave’s frequency and amplitude, and vector functions allow physicists to study the behavior of waves in a variety of different environments.
- In computer graphics, vector functions are used to model the surfaces of objects in virtual worlds. The shape of an object in a virtual world is determined by its vertices and edges, and vector functions allow computer graphics artists to create objects that are both realistic and visually appealing.
Essential FAQs
What are the key advantages of using vector functions for surface identification?
Vector functions offer a compact and versatile representation of surfaces, allowing for precise mathematical analysis and efficient computation. They provide a unified framework for representing both simple and complex surfaces, enabling the derivation of surface properties and visualization.
How do vector functions help determine surface properties?
Vector functions provide a means to calculate surface properties, such as normal vectors, tangent vectors, and curvature, at any point on the surface. These properties are crucial for understanding the local and global geometry of the surface, and they play a vital role in applications such as surface rendering and collision detection.
What are the practical applications of surface identification using vector functions?
Surface identification using vector functions finds applications in various fields, including engineering design, computer graphics, and physics. In engineering, it is used for modeling and analyzing complex surfaces, such as those found in aircraft wings or fluid flow simulations. In computer graphics, it is employed for creating realistic 3D models and animations.
In physics, it is used for understanding the behavior of surfaces in response to forces and interactions.